What if N in Art Gallery Theroem Isnt Divisble by 3

Get this book -> Problems on Array: For Interviews and Competitive Programming

In this commodity, nosotros have explored Fine art Gallery Problem in depth along with variants of Art Gallery Problem and important results.

Contents

1. Introduction to Art Gallery Problem
2. Types of Guards
3. Exploring a Few Examples
4. Solution to the Problem
5. Variants of the Art Gallery Problem
6. Results

Introduction to Art Gallery Problem

Consider an art gallery which is shaped in the form of a polygon with n vertices. In the art gallery trouble, the objective is to observe the minimum number of guards that tin can be placed inside this polygon or on its edges, such that the entire art gallery is visible to this set of guards. The guards cannot move from the vertices at which they are positioned. However, they have a vision of 360°, which means that they can run across all around them as long as a wall (an border of the polygon) does not obstruct their vision. This trouble was get-go presented by Chávtal in 1975.

In geometry, this problem is as follows: Find the minimum number of guards that need to be placed in an n-vertex simple polygon such that all points within the polygon are visible. (A polygon is a airtight shape made up of straight lines. A simple polygon refers to a polygon which does not intersect itself, and which does not have whatever holes.)

Types of Guards

There are multiple types of guards, classified on the basis of the position that they take:

• Vertex Guard : The baby-sit is positioned at the vertex of the polygon.
• Point Guard : The guard is positioned anywhere in the polygon.
• Border Baby-sit : This guard is placed anywhere forth the edges of the polygon.
• Mobile Guard : This guard has the ability to move from i point to some other. Although this type of guard is not used in the Fine art Gallery Problem, they are used in variants of the same.

Exploring a few examples

On examining the problem, it is trivial that in case of a convex polygon (a polygon which has all interior angles less than 180°), just i guard is required, and this guard can be placed in the centre of this polygon. There are multiple other cases where but one guard shall suffice, such every bit a star.

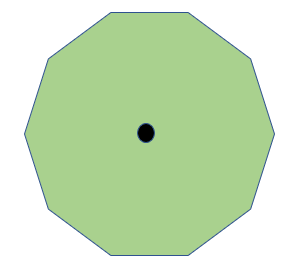
In this example, nosotros can observe that the one guard, (represented past the black dot), volition exist able to encompass the entire polygon.

At present, we find that more than one baby-sit might be required in case of a non-convex polygon (note that in some non-convex polygons, just i baby-sit volition suffice). Nosotros show one such example, where two guards are needed.

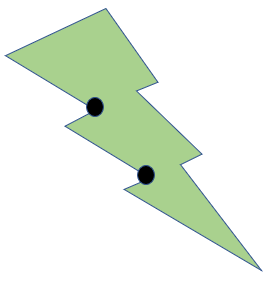
Solution to the problem

The maximum number of guards to guard the art gallery was found to be ⌊ⁿ⁄₃⌋. This solution was proposed and proved by Chávtal. However, we shall look at a more than elegant proof of the aforementioned, which was proposed by Steve Fisk. This proof uses triangulation and vertex coloring. We shall describe these in detail.

Theorem Statement

The Art Gallery Theorem is given to be equally follows:

⌊ⁿ⁄₃⌋ guards are occasionally necessary and ever sufficient to embrace an n - vertex polygon.

To prove this result, we shall first evidence a couple of sub-results, which volition then be combined to conclude the theorem.

Triangulation always exists for non-convex polygons

Triangulation of a polygon is the process of splitting it into non intersecting triangles past means of lines joining its vertices. Nosotros shall now prove that triangulation is possible for a non-convex polygon.

We prove this result using mathematical consecration. Consider the base case where northward = three. Here, the result is trivial since the polygon nether consideration is already a triangle. Now, presume the consequence is true up to polygons with northward-1 vertices.

Consider a polygon with n sides. Now, we know that the sum of the angles of this polygon is (due north-two) x 180°. Hence, the number of angles which are convex would be less than north - 2, since the sum of angles would otherwise exist greater than (northward - 2) 10 180°. Hence, at that place are at least two convex vertices. Consider the line joining these two vertices. If this line does not lie in the interior of the polygon, then slide one of its endpoints towards the other until information technology encounters a vertex. Then this line would lie within the polygon. This particular case is illustrated below:

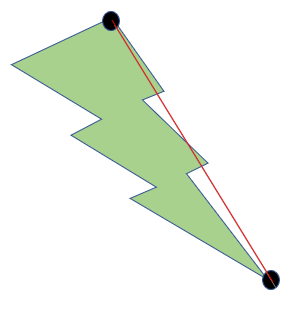
Since the entire line does not lie within the polygon, we slide the line downward until it lies in the interior of the polygon. Hence, we obtain the following:

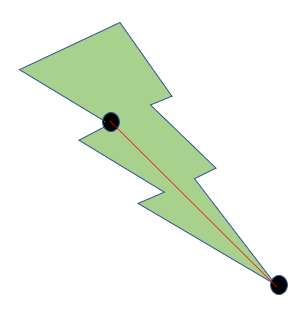
After obtaining such a line, we find that the line has divided the polygon into two smaller polygons. By hypothesis, triangulation exists for these smaller polygons, and hence exists for the unabridged polygon. Upon triangulation, the earlier example looks as follows:

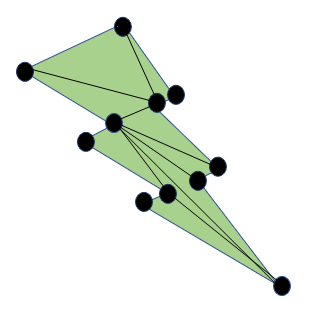
Every non-convex polygon is three-colorable

A graph is said to exist three-colorable if its vertices can be colored in such a manner that no connected vertices take the same color.

Since triangulation exists for every non-convex polygon. We proceed as follows:

• Consider any two continued vertices, and characterization them with the first and the second color.
• At present, on each triangle sharing these 2 vertices, label the third vertex with the 3rd color.
• Continue in this manner by labeling the third vertex with a color different from that of the other two vertices.

After coloring all vertices in this style, we obtain a 3-colored graph. An example of the 3 colored graph for the previous example is as follows:

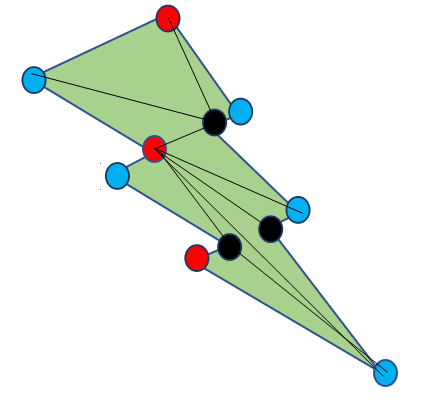
Completing the Proof

On 3-coloring the polygon, we notice that at that place is at least ane color which appears ⌊^northward⁄₃⌋ times. Hence, placing a baby-sit at each of these vertices would mean that each triangle has at least one guard, and thus the entire polygon gets covered.

Therefore, the maximum number of guards to cover the polygon is ⌊ⁿ⁄_iii⌋. Note that this result does not give any data regarding the minimum number of guards.

Variants of the Art Gallery Trouble

There are multiple variants of the fine art gallery problem, most of which have numerous applications. We shall discuss two such variants here:

• Chromatic Fine art Gallery Problem : Given a polygon, the objective is to find the minimum number of colors such that if the area covered by 2 guards overlap, so those guards do not have the aforementioned color. For this problem we have the following theorem: For every positive integer k, there exists a polygon with 3k² + two vertices such that the minimum number of colors is greater than or equal to one thousand
• The Watchman Road Trouble : In this variant, the watchman are not stationary. Instead, the focus is to find the shortest road such that the watchman is able to encompass the entire polygon. Two techniques are used to solve this trouble: essential cuts and reflection principles. This problem has multiple applications in the field of robotics.
• The Prison Yard Problem , where the guards are continuing on the edges such that both the interior and the exterior of the polygon are visible.

Results

Hither, we shall take a await at some of the results that were developed for the variants of the fine art gallery problem.

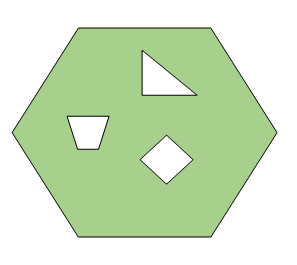
1. O'Ruke proved in 1987 that ⌊^{(due north+2h)}⁄₃⌋ are sufficient for a polygon with n vertices and h holes. A pigsty in a polygon is an region within the polygon that does not belong to the polygon. An example of a polygon with a hole is given below:

2. Kahn, Klawe and Kleitman proved in 1983 that ⌊^north⁄_four⌋ vertex guards are sufficient for an -vertex orthogonal art gallery. An orthogonal fine art gallery is ane in which all the edges are either along the horizontal x-centrality or the vertical y-axis. An example of an orthogonal art gallery is given below:

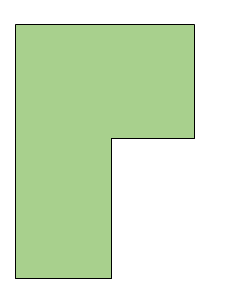
This proof uses the method of convex quadrilateralisation, which is like to that of triangulation which we followed for the classical fine art gallery problem.

3. Hoffman and Kriegel proved in 1996 that ⌊ⁿ⁄₃⌋ are sufficient to guard an orthogonal polygon with northward vertices and h holes.

4. O'Rouke proved in 1983 that ⌊ⁿ⁄₄⌋ mobile guards are sufficient for a simple polygon with n vertices and h holes.

5. Aggarwal proved in 1984 that ⌊^{(3n +4)}⁄₁₆⌋ mobile or border guards are sufficient to guard an art gallery with n vertices.

6. Gyori et al. proved in 1996 that ⌊^(3n+4h+iv)⁄₁₆⌋ mobile guards are sufficient for an orthogonal polygon with n vertices and h holes.

With this article at OpenGenus, y'all must have the complete idea of Fine art Gallery Trouble.

massinaforiever.blogspot.com

Source: https://iq.opengenus.org/art-gallery-problem/

Share this post